|
|
|
连接分为θ连接、等值连接及自然连接三种。连接运算是从两个关系R和S的笛卡儿积中选取满足条件的元组。因此,可以认为笛卡儿积是无条件连接,其他的连接操作是有条件连接。θ连接
|
|
|
|
θ连接是从R与S的笛卡儿积中选取属性间满足一定条件的元组。其形式定义如下:
|
|
|
|
|
|
其中:'XθY'为连接的条件,θ是比较运算符,X和Y分别为R和S上度数相等,且可比的属性组。tn[X]表示R中tn元组的相应于属性X的一个分量。tm[Y]表示S中tm元组的相应于属性Y的一个分量。需要说明的是:
|
|
|
|
|
|
|
|
其中:i=1,2,3,…,n,j=1,2,3,…,m,'iθj'的含义为从两个关系R和S中选取R的第i列和S的第j列之间满足θ运算的元组进行连接。
|
|
|
|
.θ连接可以由基本的关系运算笛卡儿积和选取运算导出。因此θ连接可表示为:
|
|
|
|
|
|
|
当θ为“=”时,称之为等值连接,记为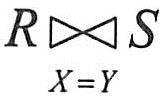 。其形式定义如下: 。其形式定义如下:
|
|
|
|
|
|
|
|
自然连接是一种特殊的等值连接,它要求两个关系中进行比较的分量必须是相同的属性组,并且在结果集中将重复属性列去掉。
|
|
|
若tn表示R关系的元组变量,tm表示S关系的元组变量;R和S具有相同的属性组B,且B=(B1,B2,…,BK);并假定R关系的属性为A1,A2,…,An-k,B1,B2,…,Bk,S关系的属性为B1,B2,…,BK,BK+1,BK+2,…,Bm;为S的元组变量tm去掉重复属性B所组成的新的元组变量为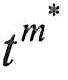 。自然连接可以记为 。自然连接可以记为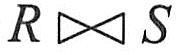 ,其形式定义如下: ,其形式定义如下:
|
|
|
|
|
|
自然连接可以由基本的关系运算笛卡儿积和选取运算导出,因此自然连接可表示为:
|
|
|
|
|
|
特别需要说明的是:一般连接是从关系的水平方向运算,而自然连接不仅要从关系的水平方向,而且要从关系的垂直方向运算。因为自然连接要去掉重复属性,如果没有重复属性,那么自然连接就转化为笛卡儿积。
|
|
|