|
|
|
|
B-树的定义:一棵m阶的B-树,或为空树,或为满足下列特性的m叉树。
|
|
|
|
|
|
|
(3)除根之外的所有非终端节点至少有 棵子树。 棵子树。
|
|
|
|
|
|
(n,A0,K1,A1,K2,A2,…,Kn,An)
|
|
|
式中,Ki(i=1,2,…,n)为关键字,且Ki<Ki+1(i=1,2,…,n-1);Ai(i=1,2,…,n)为指向子树根节点的指针,且指针Ai-1,所指子树中所有节点的关键字均小于Ki(i=1,2,…,n),An所指子树中所有节点的关键字均大于Kn,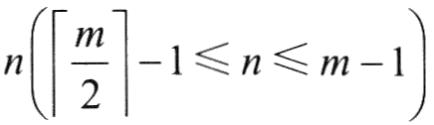 为节点中关键字的个数。 为节点中关键字的个数。
|
|
|
|
(5)所有的叶子节点都出现在同一层次上,并且不带信息(可以看作外部节点或查找失败的节点,实际上这些节点不存在,指向这些节点的指针为空)。
|
|
|
|
B-树上进行查找的过程是:首先在根节点所包含的关键字中查找给定的关键字,若找到则成功返回;否则确定待查找的关键字所在的子树并继续进行查找,直到查找成功或查找失败(指针为空)时为止。
|
|
|
B-树上的插入和删除运算较为复杂,因为要保证运算后节点中关键字的个数大于等于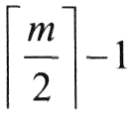 ,因此涉及节点的"分裂"及"合并"问题。 ,因此涉及节点的"分裂"及"合并"问题。
|
|
|
|
在B-树中插入一个关键字时,不是在树中加一个叶子节点,而是首先在低层的某个终端节点添加一个关键字,若该节点中关键字的个数不超过m-1,则完成插入;否则,要进行节点的"分裂"处理。"分裂"就是把节点中处于中间位置上的关键字取出来插入到其父节点中,并以该关键字为分界线,把原节点分成两个节点,"分裂"过程可能会一直持续到树根。
|
|
|
在B-树中删除一个节点时,首先找到关键字所在的节点,若该节点在含有信息的最后一层,且其中关键字的数目不少于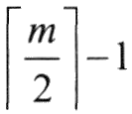 ,则完成删除;否则需进行节点的"合并"运算。若待删除的关键字所在节点不在含有信息的最后一层上,则将该关键字用其在B-树中的后继替代,然后再删除其后继元素,即将需要处理的情况统一转化为在含有信息的最后一层再进行删除运算。 ,则完成删除;否则需进行节点的"合并"运算。若待删除的关键字所在节点不在含有信息的最后一层上,则将该关键字用其在B-树中的后继替代,然后再删除其后继元素,即将需要处理的情况统一转化为在含有信息的最后一层再进行删除运算。
|
|
|
|
|
|
|
|
|
|